While the in-place flooding method is reliable and easy both to understand and implement, you may want to opt for a faster algorithm.
You can create a queue in memory and deal with each cell once only. The code to do this is a little more complicated and you will need up to 256 bytes of additional memory. The payoff is in performance. The method described below will be 20 to 50 times faster for typical mazes.
There is no absolute need for fast solving but I can see how cutting the total time for a solve cycle from, say 0.5 seconds to 10 milliseconds would be a worthwhile improvement.
We will call the queue the frontier. You will see why when you look at the sequence shown below. As the maze is flooded, a wave front expands outwards from the target cell. It is only these cells that we actively deal with in the queue. As soon as the frontier reaches the starting cell, we are done flooding.
In general, the starting cell is any cell. To solve the whole maze, set the starting cell to the first cell in the maze. To reverse your path, set the target to the first cell and the starting cell to be the centre or your current location.
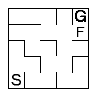 |
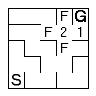
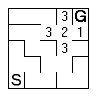
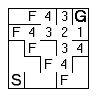
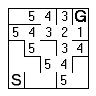
Using the second method, first mark any cells that are adjacent to and reachable from the goal as frontier cells. Flag them and added to a queue of cells to be processed. | 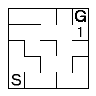 |
While there are cells in the frontier queue, process each one. The contents of each is replaced with the distance to the goal (either stored in the frontier queue or calculated from the neighbours as you go. |
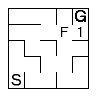 |
The replaced cell then has its neighbours marked and placed in the frontier queue. | 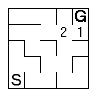 |
The frontier moves toward the start and the visited cells fill with numbers. |
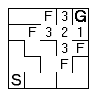
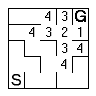
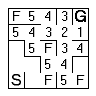
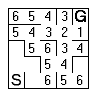
The next sequence shows the rest of the maze being flooded.
 |
 |
 |
 |
 |
 |
 |
 |
 |
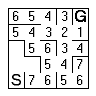 |
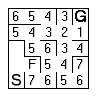 |
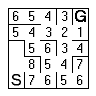 |
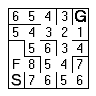 |
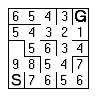 |
You can clearly see how dead ends are handled and what happens when there is more than one way through. You will need to be careful about not adding a cell twice to the frontier list. | |
| Once the frontier reaches the start cell you are done. The shortest route that you know of is now traced by simply moving to the neighbouring cell with the lowest value. | |||
The algorithm will look something like this:
create and initialise a queue with 256 elements
create a routing map as an array of 256 bytes
fill the array with the value 255
fill the target cells(s) with the value 0
add the target cell locations to the queue
while there are items in the queue
get a location from the tail of the queue
if the cell does not contains the value 255 then
for each accessible, unfilled neighbour
put in it a value one more than the current cell
add it to the queue
end for
end if
end while
You can run this algorithm as often as you have processor time for.
There is actually no need to run it any more often than when you are in a junction cell and you want to decide which way to go.
One way to optimise your route for a speed run is to assign different weights to the neighbouring cells depending on whether you will have to turn to get to them and so on. With a fast flooder/solver, your mouse could try several strategies with test fills to determine the best possible route.
Hiii..I want to make a micro mouse so i started searching for maze solving algos and found this one..got nice info here..thanks for providing this much info for us…
I am doing a report about micromouse and plan on one day being apart of a team. This is a great bunch of information
Ty.
Interesting concept but I found it doesn’t work in practice for mazes where the destination is the center cell. Instead I looked for the check where the current cell that the mouse is occupying has been assigned a flood fill number, this massively reduces the iterations of the algorithm as the mouse approaches the destination cell.
In what way did it fail to work?
I have used this without any trouble. It is true that you can make it faster by only flooding out as far as the current mouse location. However, I flood all the way to the start so that I can test whether the mouse has enough information to finish the search early and return for a fast run.