Effect of wheel slip on position
Suppose your micromouse is travelling in the maze at a steady speed. If there are breaks in the walls to left or right, and the mouse is correctly positioned you would expect the breaks to be seen every 180mm for a classic mouse. It seems obvious to use the detected wall breaks to correct for…
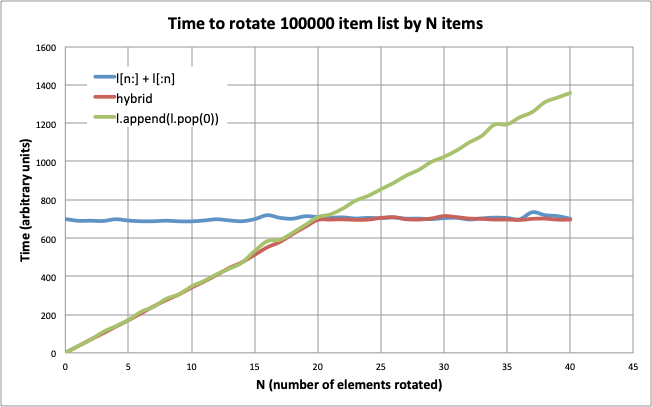
Efficient rotation of a list in Python
Efficiently ad new items to a Python list when plotting real time data.
2nd International Symposium on Micromouse
Call for Papers The 2nd Micromouse Symposium 1st May 2020, Vila Real, Portugal, the 2nd International Symposium on Micromouse, will be held in Vila Real, Portugal, 1st May 2020. Industry experts, researchers and academics are expected to gather together to share ideas and experiences surrounding frontier technologies, breakthroughs, innovative solutions, research results, as well as initiatives related…
Micromouse in Mumbai
From Abinav Kumar: The Indian Institute of Technology, Bombay is regarded as one of the premier institutes in India for imparting education of one of its kind and to provide resources for the cutting edge technology recognized all over the world. Techfest is IIT Bombay’s annual science and technology festival to promote technology, scientific thinking, and innovation and has…
Micromouse contest in Egypt – an invitation
From Mohamed Orabi : “We are organizing a new micromouse competition during the IEEE Conference on Power Electronics and Renewable Energy, that will be hold during Oct. 23-25, 2019 in Aswan, Egyptwww.ieee-cpere.org We would like to invite teams from world wide to participate. To encourage team, The conference will provide each team with free registrations…
Time taken to run a straight
Calculating the time needed to run a straight between two turns in the micromouse contest