NB: there seems to be an error in these calculations. …
In a normal tricycle mouse, the driving force will come through the rear wheels and a single front wheel will be used for steering. To a certain extent this can allow you to decouple the steering from the drive mechanism and control loops. Tricycles can be good for acceleration. As the power is applied, reaction torque will transfer weight to the rear, driving wheels giving you an increase in traction. If you overcook it however, the steering wheel may lift off the ground and your steering is gone. on the other hand, deceleration is a bit of a problem as weight transfers to the front of the mouse and the available braking force from the drive train is reduced. Remember that you cannot brake as hard as you can accelerate and all the bits of your mouse are more likely to stay attached.
Here is a diagram of a tricycle mouse:
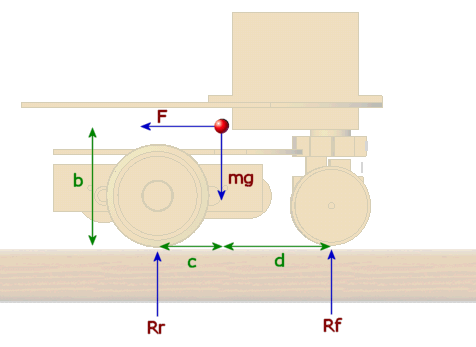
- The red dot is the centre of gravity, distances are in green.
- m is the mass of the mouse
- Rr and Rf are the reaction forces for the rear and front wheels. That is, the weight on the wheels. The rear wheels are treated as one for now.
- F is the force applied to accelerate the mouse. It points that way to represent a restraining force that would hold the mouse stationary for the purposes of analysis
- g is the acceleration due to gravity.
So, lets see what the mouse can do.
Assume for the time being that we have plenty of friction between the driving wheels and the floor, what is the maximum acceleration that we can apply before the front wheel leaves the ground in a spectacular display of foolishness.
At that point, the sum of the moments about the point of contact between the ground and the rear wheels will be zero. Thus:
Fb – mgc = 0
From Newton, F = ma, where a is the acceleration of the mouse
mab – mgc = 0
ab = cg
a = cg/b
For my mouse (litmus), b = 24mm, c = 10mm so
a = (10/24)g
a = 0.42g
a = 4.1m/s/s
This is not world class performance but is more than the existing motors can manage and would be quite satisfactory for now. Later we shall see if there is enough friction for this acceleration anyway. When I first put it together, I put the batteries over the motors. That reduced c to about 3mm and the maximum acceleration to about 0.125g. Well, there was certainly enough motor torque and more than enough friction as litmus did an instant wheelie across the floor with me in frantic pursuit. As ever, there are confilicting design requirements. The CG needs to be low. That can be achieved and I may be able to reduce it to about 20mm which would increase the maximum acceleration to around 0.5g. To allow it to turn in the maze, the mouse needs to be short. However, for best acceleration (and worst deceleration), the CG needs to be well forward. If you place the CG a long way from the driving wheels, the moment of inertia becomes large and you need bigger motors
Right, what is the maximum acceleration we could achieve for a given coefficient of friction? Now, the maximum force that can be applied to accelerate the mouse is:
F=µRr
To find the value of Rr, we take moments about the front wheel. These will sum to zero:
mgd – Rr(c+d) + mab = 0
Substitute
Rr = F/µ
Rr = ma/µ
to get
mgd – ma(c+d)/µ + mab = 0
µgd – a(c+d) + µab = 0
µgd = a(c+d-µb)
a =µgd/(c+d-µb)
Rather than solve for µ, we can draw a graph of a as a function of µ, given d = 40mm, c = 10mm, b = 24mm
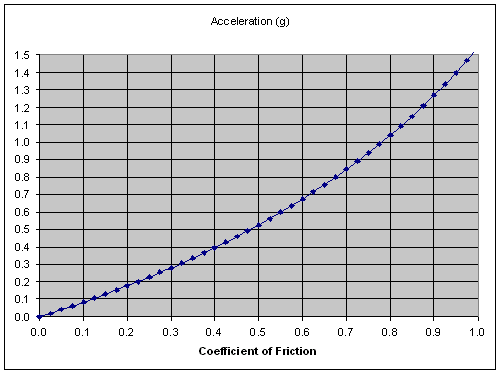
You can see that, to get an acceleration of 0.4g only requires a coefficient of friction of about 0.4. This should be easily obtainable with rubber tyres on painted wood. Usable coefficients of friction for rubber tyres on paint are in the range 0.5 to 0.8 giving us a potential acceleration range of around 0.5 to 1.0g for litmus (if we can keep the front wheel down).
From these calculations, I conclude that:
- I am more likely to flip this mouse over than suffer wheelspin when accelerating
- My maximum acceleration should not exceed 4.1m/s2
- I could do with getting the center of gravity lower
- A shorter mouse is easier to accelerate and turn but runs the risk of a wheelie
- As the CG moves forward, we get less chance of a wheelie but poorer acceleration due to reduced grip by the driving wheels.
- Short, small tricycles will have performance limitations that may make them uncompetitive at top level