The moment of inertia of a micromouse is a useful number to know. It tells you how easy or hard your mouse will be to turn and lets you calculate an appropriate value for the angular acceleration during the lead-in and lead-out of the turn. Indeed, you may find out the upper limits or what your mouse can achieve. the race is, after all, won in the turns they say. So, how can you find out what the moment of inertia is for your mouse?
One way is to calculate it. Simple shapes have easy to understand moments of inertia. You can find a good set of examples on this wikipedia page. here are plenty of simple geometric shapes and their moments of inertia. However, I don’t suppose your mouse corresponds to any of those shapes. It turns out that moment of inertia is all about how far the mass or masses of an object are from the centre of rotation. For example, imagine a short rod with a couple of weights at the end. If the rod were suspended by its mid-point so that the rod were horzontal, you could spinn the rod around fairly easily and stop it fairly easily. Now use the same weights but at the end of a rod that was twice as long. This longer rod would be harder to get spinning and harder to slow down. The further the mass is from the centre, the higher the inertia.
This observation is critical to good micromouse design. Two mice, each of the same weight, but having their mass distributed differently will perform differently. To calculate the moment of inertia of your mouse, you would have to weigh all the component parts, measure or calculate their distance from the centre of the mouse and add up all the individual moments of inertia to come up with a total for the mouse. This is clearly not going to be easy to do and the result will be an estimate at best. You could, for example, work out the contribution of the motors quite easily but what about all the components on the main board? A good mouse design will place as much weight as possible close to the centre. Many builders work hard to get the moment if inertia as small a possible.
Since it is relatively hard to accurately calculate the moment of inertia, how about measuring it? This turns out to be surprisingly easy. You may have seen clocks that, instead of a swinging pendulum, have a set of weights that rotate around a vertical axis instead. This is an example of a torsion pendulum. The object that you want to get the moment of inertia for is suspended from, typically, a wire that can twist. If you start it off with a twist, it will oscillate back and forth with a period that depends upon the moment of inertia of the object and the stiffness of the wire – and nothing else.
You might like to find out more about torsion pendulums at one of these pages:
Making your own torsion pendulum is quite easy. Essentially, the key component is a piece of piano wire about 1m long. Steel guitar strings should work well. String, fishing line and copper wire will all work but they are quite lossy and the oscillations will damp down quite quickly. For best results, you need something that is not too stiff so that the oscillations are relatively slow. This improves the accuracy. Apart from the suspension wire, you need a cradle to hold your object under test. That cradle will have its own inertia so you must first calibrate your equipment.
For my experiments, I made a imple frame to hold the mouse and some test massess for calibration. It is importat that you are able to mount the objects as closely as possible to the rotational axis of the setup.
The wire used to suspend the frame is fixed to the top of a door frame so rotation is only possible by the wire twisting. the equation describing the oscillation of this type of pendulum is very simple:
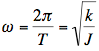
Where k is the spring constant, J is the moment of inertia of the suspended mass and T is the period of oscillations. Apart from the mouse, we have two unknowns – k and the inertia of the frame. We can work both out by doing a couplel of calibration runs. I took a couple of weights – steel and aluminium discs – that I had in the garage. These are placed on the frame and ten complete oscillations are timed to the nearest tenth of a second. Divide this by ten to get the length of one period to about one hundredth of a second. Since I know the mass and dimensions of my objects, and I have two of them, I can calculate the total inertia of the system with each of the weights and use that to find the value of k and the inertia of the frame. The latter is easy because, as long as the test objects are carefully placed, the total inertia of the system is the sum of the inertias of its components and I know the moment of inertia for the test weights very accurately. Test the accuracy of your experiment by working out the inertia of a third object that you can accurately calculate the true inertia of.
Once you are happy that the setup is working, it is relatively straightforward now to place your mouse carefully and centrally on the frame and measure the time for ten complete oscillations. Now that you know the stiffness of the spring and the inertia of the frame, it is easy to calculate the moment of inertia of your mouse. So esy in fact that it took less time to make the frame, do the calibration and measure the inertia of my two mice than it did to write this page.
For the record, my results are:
Decimus 1:
mass = 174g
moment of inertia = 125.6 x 10-6 kgm2
Decimus 2:
mass = 112g
moment of inertia = 99.3 x 10-6 kgm2
Without getting carried away with analysis, I estimate that the accuracy is better than 5% and, with good experimental technique and electronic timing could easily be improved to about 1%
If you work out the moment of inertia of your mouse, I would be glad to see the results in the comments. Especially if you can compare a measured result to a calculated result.
