When you turn corners in the maze, you can do so with an in-place turn or an integrated or smooth turn.
In-place Turns An in-place turn means coming to a halt, spinning on the spot and setting off again. All this will tend to be time-consuming although relatively easy to perform. The rate at which your mouse can spin will depend upon the available torque, wheel friction and the inertia in your mouse design.
Integrated Turns Integrated turns are rather more difficult to do well. Approach and exit speeds must be carefully calculated and the velocity profiles for the two wheels is far from obvious and not too easy to calculate. In return for the extra complexity, you get smooth, fast turns which look really good and give you real competitive advantage.
How fast? If you go too fast around a corner, two things are possible. First you might lose grip with the maze floor and skid. Clearly, this is less than good. You can no linger rely upon your odometry data. The situation may be recoverable if you have not overdone it. Nevertheless, you don’t see many mice doing handbrake turns around tricky corners. The second outcome is that you may tip over. Now this is would be the end of the race for you so it would be best avoided. Automatic recovery from such an accident would be pretty clever.
Lets have a look at the two possibilities, and decide which is the more likely and what the consequences are for the race. Bear in mind that these are models – simplifications to give some idea of the numbers.
Skidding Your mouse exerts a force on the floor due to gravity. When it corners there is an additional force due to centripetal acceleration. Just at the instant of a skid, these forces will be equal. The centripetal force depends upon the mass of the mouse, the square of the velocity and the radius of the turn:
![]() The opposing force is determined by the mass of the mouse and the coefficient of static friction of the tyres on the floor
The opposing force is determined by the mass of the mouse and the coefficient of static friction of the tyres on the floor
![]() Equate these and rearrange to find the maximum velocity at which you can get around a constant radius turn without skidding.
Equate these and rearrange to find the maximum velocity at which you can get around a constant radius turn without skidding.
![]() ote that the mass of the mouse is not a factor here. Assume we have a right angle turn with radius 0.09m and a coefficient of friction of 0.7 (not too far out for rubber on wood – check yours). This gives us a maximum velocity of about 0.78m/s. The distance around the turn is 0.141m and so the turn will take 0.18 seconds.
ote that the mass of the mouse is not a factor here. Assume we have a right angle turn with radius 0.09m and a coefficient of friction of 0.7 (not too far out for rubber on wood – check yours). This gives us a maximum velocity of about 0.78m/s. The distance around the turn is 0.141m and so the turn will take 0.18 seconds.
With the coefficient of friction at 1.0, the maximum speed around a 0.09m bend would be 0.94m/s before you get to slide out. While increasing the coefficient of friction for your tyres has great benefits, you are chasing a law of diminishing returns in terms of cornering speed. It has been said however that the race is in the turns. Racing down the straights is relatively simple.
Don’t worry about the outer wheel travelling faster. During the turn, weight is transferred more to the outer wheel and the equations all work out just the same. Remember how the mass of the mouse was not present in the equation?
Tipping
So, weight gets transferred to the outer wheel. What happens if we try and corner so fast that we are in danger of tipping up. How easy this is will depend upon how high your centre of mass is. It should be apparent that a tall mouse with a narrow wheel track will be more likely to tip over. Call the height of the centre of mass H and the wheel track (distance between the wheels) D. The weight of the mouse, W, acts downward through the centre of mass and the centrifugal force, F, acts radially outwards through the centre of mass, parallel to the maze floor.
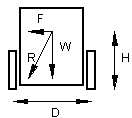 o long as the resultant, R, of the two forces is within the wheel track, we will not tip over. We have already seen that the value of F is given by
o long as the resultant, R, of the two forces is within the wheel track, we will not tip over. We have already seen that the value of F is given by
![]() By examining similar triangles, you should be able to see that, at the moment of tipping over
By examining similar triangles, you should be able to see that, at the moment of tipping over
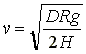 As an example, my mouse has a wheel track, D, of 75mm and the centre of mass is about 45mm above the ground. Substituting into the equation we get
As an example, my mouse has a wheel track, D, of 75mm and the centre of mass is about 45mm above the ground. Substituting into the equation we get
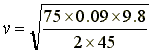 Which give v = 0.86m/s (the inappropriate units cancel out)
Which give v = 0.86m/s (the inappropriate units cancel out)
Since I should only be able to do about 0.78m/s before the tyres slip, falling over will not be a problem for me. To be honest, if I could make it go fast enough so that I was anywhere near either limit I would be very happy indeed. A rather better built mouse with a centre of mass, say , 25mm from the floor and a wheel track of 90mm might be able to manage 1.26m/s before tipping.
Before your mouse gets to tip over, even if it does not slide on the ground, you may lose traction on the inner wheel with pretty disastrous consequences for your odometry.
Or, to summarise,With a moderately sensible mouse design, you will not tip over before you skid out of control (unless you hit something…). If you want a real speed machine, you will need to get the centre of mass down as far as possible. It should not be too hard to get it down to 30mm or so which, for the example above, improves your maximum cornering speed to about 1m/s
In calculating maximum speed so that friction balances centripetal force, how do you find the radius of curvature for your turn??
You may find what you need here:
https://micromouseonline.com/book/micromouse-book/robot-dynamics/smooth-corners