Easier Statistics for Sensor Data

Learn how you can calculate the standard deviation, or spread, of your sensor readings on-the-fly while collecting data without having to first record all the values and then do the statistics.

Statistics based on the data from your sensors can tell you a lot about the system and the environment it is working in. Most of the methods for calculating suitable results need you to record a lot of data and then process that later. If all you want is an average and some measure of spread, such as standard deviation, then you can actually calculate that while collecting the data and without having to store any of the data values. Back in school, you may have been taught how to calculate the mean (average) of a set of data and, possibly the standard deviation or variance.

The mean

The mean is pretty easy. You just add up all the values and divide by however many you have. Suppose you collect $N$ readings of a value, $x$ , and you want to work out the mean. You can write the formula for this like so:

$\overline{x} = \frac{\sum x}{N}$

Here, the $\sum{}$ symbol just means ‘the sum of’ and so the formula reads as ‘the sum of the values of $x$ , divided by $N$ , the number of values’.

The Standard Deviation

So far so good. Now, what about the measure of spread. That is, how spread out are your values? For this, a common measure is the standard deviation, generally shown with the symbol $\sigma$ .

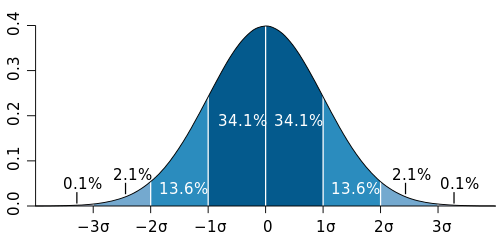
Standard deviation is a descriptive statistic. Feel free to look up the details in the references below. For now, remember that, assuming your data is actually random and follows a normal distribution, you can assume that about 95% of the values will all fall within $\pm2\sigma$ . For example, suppose we take a bunch of readings from a temperature sensor which is affected by noise. We calculate the mean value as 1438 and a standard deviation of 24. We can say that 95% of our readings are inside the range (1438-48) to (1438_48). That is, between 1390 and 1486. You might reasonably suppose that is a lot of noise. It probably is if you are using a 12 bit ADC. That would make the standard deviation 24 LSBs. Bear in mind that noise levels are something that have to be considered within the context of the system being measured. Here the standard deviation is about 13% of the mean. if the noise were in the measuring system and the mean was, say, 400, then the standard deviation would be 24% and you might be more worried. Clearly, though, a small value for standard deviation is a good thing. In the diagram below (from Wikipedia) the mean us given the symbol $\mu$ which is a common usage.

Note also that, since the probability of actual results falling further than $3\sigma$ from the mean is very small, they can either be ignored as outliers in your system or an sign that something else is going on that needs your attention.

In school, or even at college, you may have been taught how to calculate standard deviation from a formula like this:

$\sigma = \sqrt{\frac{\sum (x - \overline{x})^2}{N}}$

Assuming you are not a big fan of maths, this just means: “for each data value, x, calculate the difference between that and the mean; square the result; add up all those values; divide by the number you have; take the square root”. Easy. For an embedded system like a micromouse, there is a, problem though. You have to store all the data first and then calculate the result. And that means two passes through the data because you need to know the mean before you can calculate the standard deviation. But what if you don’t want to wait. Or what if you don’t have much RAM to store the data. Well, there is a way to get the same answer without having to store all the data.

The formula for standard deviation can also be written like this:

$\sigma = \sqrt{\frac{\sum x^2}{N} - (\frac{\sum x}{N})^2}$

Right now, this may look worse but bear with me. This formula says the standard deviation is calculated only from the sum of the values, $\sum x$ , and the sum of their squares, $\sum x^2$ . These are accumulated as we take samples. Every time we read the ADC, all that you need to do is to add the value to a variable, sumX, then add the square of that value to another variable, sumX2.

Whenever you want to know the standard deviation, just do the calculation above. For example, on my mouse, I can have the systick interrupt accumulate the values of $x$ , and $x^2$ as long integers and use floating point calculations just to calculate the result.

Sample Code

Here is a code fragment that should illustrate the method. Although only 1000 numbers are generated, for illustration, the principle is the same. Note that you will need a large variable to accumulate the sum of squares. If your processor makes it easy, make the accumulators floats in the first place. If you run long enough even these will overflow though

#include "time.h"
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
// dirty hack to generate a number centred around 2048 with
// an approximately normal distribution.
// use a larger count for a smaller standard deviation
int getData(void){
  int32_t result;
  int i;
  int count = 1000;
  result = 0;
  for (i = 0; i< count;i++){
    result += rand() % 4096;
  }
  return result / count;
}

int32_t x;
int32_t sumx;
int64_t sumx2;  // note that this needs to be able to hold BIG values
float mean;
float standardDeviation;
int32_t sampleCount;

int main(int argc, char** argv) {
  int i, n;
  // if you want different random numbers each time this is run
  // uncomment the line below
  srand(time(NULL));
  n = 0;
  sumx = 0;
  sumx2 = 0;
  for (i = 0; i < 1000; i++) {
    n++;
    x = getData();
    sumx += x;
    sumx2 += (int64_t)x*x;
    printf("%6d\n", x);
  }

  mean = (float) sumx / n;
  standardDeviation = sqrtf((float) sumx2 / n - (mean * mean));
  printf("     sum of X = %12d\n", sumx);
  printf("   sum of X^2 = %12ld\n", sumx2);
  printf("         mean = %12.4f\n", mean);
  printf("standard dev. = %12.4f\n", standardDeviation);
  return (EXIT_SUCCESS);
}

For serious use, you may want to look at more accurate ways to calculate some of these things. In particular, should you try to do the calculations as integers, you will want to look out for rounding errors and the order of operations would want some attention to avoid loss of precision.

None the less, this is a quick, easy way to get a running view of the mean and standard deviation of a set of observations while you run an experiment and possibly adjust values or whatever. Be careful to prevent overflows in the accumulated values and the calculations.

If you want to get a running view of the last so many values, you will need a slightly different method as outlined in the hackaday post that refers to this site:

Statistics on the Arduino

For (much) more on means, standard deviations, random numbers and statistics try these links:

The Standard Deviation

Sample Code

You Might Also Like

Decimus data – 2

Effect of wheel slip on position

Micromouse POV

Leave a Reply