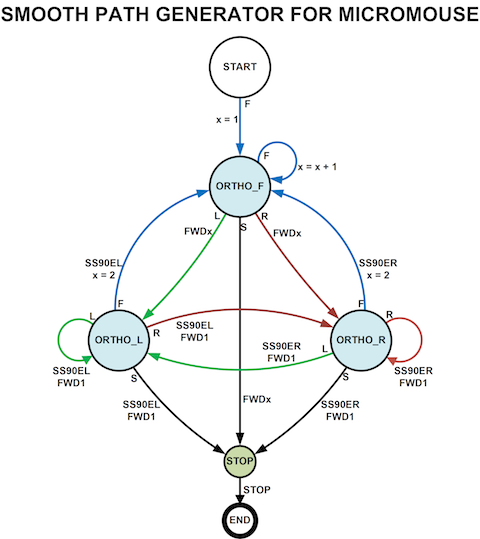
A competitive micromouse must run a path made up of smooth turns rather than stopping for in-place turns. For novice builders of micromouse, this can seem a difficult task. Here is a method for creating a smooth path using data from flooding the maze.
The method described here for generating a smooth path for a micromouse uses a state machine. If you are not familiar with these then it might be a good idea to have a look at this previous post about state machines.
Solve the Maze
The starting point is to solve the maze. That usually means some process that puts values into an array. The values make it clear which cell should be next when running the maze. A common way to do this is a flood fill. Each maze cell has a number which is the cost of getting from that cell to the goal. Another way might place a value in each cell that tells the mouse which direction will get the mouse to the goal. You can find a little more about solving the maze here: Faster Maze Solving.
Simple Paths
Either way, that information must then be converted into a series of basic instructions to the mouse. I like to put those instructions into an array as a string of characters. To follow the path, the mouse keeps taking characters from this list and executes them one by one. Only four instruction types are needed.
F – move forward one cell
R – turn right 90 degrees in place then go forward one cell
L – turn left 90 degrees in place then go forward one cell
S – stop moving
So a simple path might be stored as a string like this “FFRFFFLRFLFFS”. Storing the instructions in a string is convenient. Strings use one byte per instruction and are easily stored and manipulated in pretty well any language. Also, it makes mouse development a bit easier – especially if a team is involved. By writing a command processor, a developer can concentrate on just the task of making the mouse follow a set of instructions. Test paths can easily be generated and tested independently of tasks like searching and solving. All the command processor need do is start at the beginning of the string and work through to the end. For every character in the string, there is a simple action. It should be clear that each action can be executed in a single function or subroutine in your chosen language.
Improving Performance
Now, a mouse executing these simple instructions would not be going very fast or very smoothly. Long straights would be a series of short one cell moves. A big improvement the would be to combine some of these instructions. The simplest approach is to read through the command list, counting up all the ‘F’ instructions so that they can be combined into a single straight. The in-place turns can be converted into single, smooth 90 degree turns. The resulting path would be faster and smoother with the mouse not having to stop until it reached the goal. This is not a difficult task but it is worth doing well because it paves the way for more complex paths later.
There are a few things to look out for:
- The smooth turns need to take place completely within one cell or the mouse will not be able to execute a series of left-right-left turns.
- Every in-place turn carries with it an implied move forwards by one cell.
- Because the turns do not happen in the centre of each cell, each straight move will be shorter than just the number of cells times the length of one cell.
- Each turn has a start offset – how far before the cell centre the turn must start – and a finish offset – how far after the cell centre the turn will finish. A straight, between two turns, has to have these start and finish offsets subtracted from its total length.
A command language
The new, smooth path is itself just stored as a string. The instructions are simple and only a single byte is needed to distinguish all of the possible instructions a micromouse might need to execute. To make things easier to read in the program, I give each instruction a symbolic name.
STOP – come to a halt
FWD0 – move forward zero cells (never used directly)
FWD1 – move forward one cell
FWD2 – move forward two cells
:
FWD15 – move forward 15 cells
IP90R – in place 90 degree turn right
IP90L – in place 90 degree turn left
IP180R – in place 180 degree turn right
IP180L – in place 180 degree turn left
SS90ER – straight to straight 90 degree smooth turn sharp right
SS90EL – straight to straight 90 degree smooth turn sharp left
The values stored for each of these are carefully determined to make life easier for the command processor. For example, each turn has a left and a right version. The angle is always a multiple of 45 degrees. Then I can have a single function that does the turn. Inside that function I can examine the single byte that makes up the instruction and easily decide what direction to turn and how far. In the same way, the command for forward movement use the bottom five bits for the number of cells to move forwards. That means that simple arithmetic can be used to work out some moves. For example, FWD12 is the same as (FWD0 + 12) The dummy instruction FWD0 makes this easier later.
The 90 degree smooth turns SS90ER and SS90EL are special turns that start and finish within the same cell of the maze. The E stands for ‘Explore’ and these are the turns used by the mouse when exploring the maze for the first time.
So – how to build the smooth command list from the simple command list? I need to go through the simple commands, one at a time and, for each one, perform some kind of action. A bit of thought should bring these observations for a valid path:
- The simple commands always start with an ‘F’.
- They always always end with and ‘S’.
- The length of a straight cannot be known until its end is found.
- Every turn in place has an implied straight after it.
Translating instructions
The translation code must have a way to produce an output that depends on the current input as well as the history of what went before. That is to say, the output depends on the current input and the current state of the path. This is a state machine. In fact it is a particular kind of machine called a Mealy Machine. State machines are conveniently represented in a diagram. I have an earlier page explaining more about State Machines.
The state machine
In this state machine, only two kinds of action are used. A variable, x, is updated or instructions are added to the output list. The variable is the number of cells that a straight will cross. A start and stop state are identified so that variables can be initialised and the end point identified. To keep things simple no account is taken of any errors caused by illegal input characters or a missing terminator. Clearly, the implementation code will have to do that. However, each possible input character should have a corresponding action. Running the machine involves keeping track of which state the machine is in and looking at the next input character to see what to do next. This is a more complex state machine than those shown before. The point of the state diagram though is that you can sit down with your input data and work your way through the diagram, step my step. At each step, you have a simple decision and a simple output. When you reach the end, the job is done. It takes very little thought and the corresponding code is also very simple in structure.
An example
Suppose there is a small maze with a solution that gives the simple path “FRFFLFRLS”.
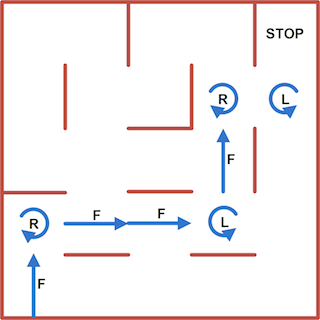
The machine initialises x to have the value 0 and moves to state ORTHO_F. Take the first character from the simple path and follow the appropriate arrow. If it is an ‘F’, just add one to the cell count. If it is a ‘R’ or ‘L’, the forward move ends and a turn begins. The forward move length is now known and so an instruction is added to the output list. No turn is yet output – it should become more clear later why that is so. For now, the state machine is in state ORTHO_R since that is the first turn character found in the simple path. The next character found is another ‘F’. The state machine adds an SS90ER instruction to the output and sets the variable x to the value 2 and moves to state ORTHO_F. Why two cells after a turn? Well, each in place turn has an implied forward after it and an ‘F’ was just found on the input so that is two cells altogether.
With the state machine in state ORTHO_F, the next command is ‘F’ and the distance counter, x, is incremented to the value 3. Following that is a ‘L’. A 3 cell straight will be added to the output, and the machine moves to state ORTHO_L. There is another short straight followed by a ‘R’ and the machine will be in the ORTHO_R state.
Instead of ‘F’, the next command is ‘L’. The state machine must now output a single cell straight and move to state ORTHO_L. Notice how the value that the cell count is set to will depend upon the instruction that comes next. Until it is seen, the machine cannot know exactly what to do. That is why it is not safe to immediately output a turn instruction as soon as one is seen. After this last turn, the path stops and a final straight is output. Every path starts and ends with a straight.
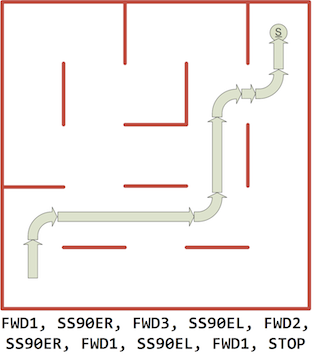
For practice, start with the simple path “FRFFLFRLS” and work through the state machine, step by step. The result should be the new path
FWD1, SS90ER, FWD3, SS90EL, FWD2, SS90ER, FWD1, SS90EL, STOP.
The new path looks like this:
In this state machine, no account is taken of errors in order to keep the diagram fairly simple. The implementation code does account for errors in the input data. You can find sample code and test cases here:
https://github.com/micromouseonline/smooth-pathfinder
Generating Diagonal Paths
If you have got this far, you may feel this is a lot of effort for what looks like an easy job. Much less easy is the business of generating a path that makes use of diagonals. It turns out that all that is needed is a bit of thought and the same state machine can be extended to do that job very easily.
Hi Peter,
Great article! I’m still a bit confused on how to approach exploring the maze using a scheme like this. It seems that it would be difficult to do non-stop searching.
This is under the assumption that I have a lateral and rotational controller separately. Any suggestions?
Thanks!
This is not really about the exploration phase. You would use this after exploration to generate a good fast run path. OR, while exploring to get a path for the mouse to run quickly towards home or an unexplored section of the maze.
When exploring, you are more concerned with what happens in each cell. The simplest approach is to start the mouse moving, wait until you are crossing the cell boundary, look at the walls, decide what direction to turn, turn, rinse and repeat until you get to the goal.
Oh okay. Thanks for your reply.
The reason I ask, is I was trying to think of a way that would allow an easy expansion to later movements, such as Min7. It looks like it explores cell by cell, but when it needs to check a cell that is far away, it does a “mini-speedrun” even running diagonals while exploring!
then what you can try is this. When it comes time for the mouse to decide which way to turn, it can do the flood and generate a path to the goal but instead of ending the path at the goal, end it at the first unvisited cell on the way. Then execute the command list up to that point. The mouse will then do a fast run to the unexplored cell where it can continue as before.