Some time ago, I wrote about a way to work out your position when following a line based on the readings from a set of reflctive sensors. The method was a bit complicated and I was never happy with it. This should be a much better setup.
I should point out right from the start that I have not tried this yet. First, consider how to set up the sensors. Typical line follower contests have the robot follow a 19mm white line on a black surface. The apparently odd line width seems to come about because the contest originally used 3/4 inch tape and 19mm is what you now buy. Quite why nobody ever rounded it up to 20mm is beyond me.
While we could set up sensors so that they treat the presence of a line as a binary value, we can do better if the sensor gives a direct value indicating how much of the line it can see. The idea is that, with the sensor directly over the centre of the line, the value is at its maximum and the reading falls of to 50% when the sensor is directly over the line edge. The variation in reading will not be linear because you are effectively measuring the area of a segment of a circle formed by the emitter shining on the floor. For the purposes of modelling, I have assumed a bell shaped curve for the response, looking like this:
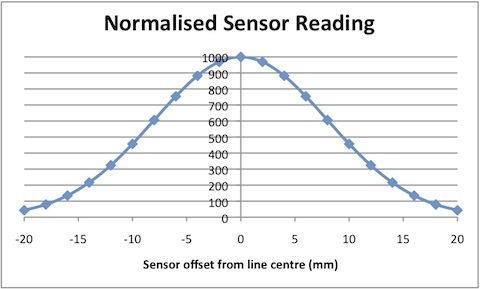
This shape is a portion of a normal probability distribution. As such it has certain desireable properties. Real sensors may vary from this a lot but the sensor design should be aimed at getting a response as close as possible to this for best results. This may ne possible for carefully chosen combinations of emmitters and detectors as well as their orientation with respect to the floor.
Each sensor will need to be normalised to give a particular value, 1000 in this case, when central over the line and close to zero when over continuous black. Since the sensors will vary, the simplest way to achieve this is to have the follower rotate on the spot through a full circle while centred over the line. Each individual sensor should get two chances to register a maximum response which can be stored for normalising individual readings while running. By also recording the minima, the full range of responses can be used to best effect.
The array of sensors consists of six devices, mounted at 15mm intervals. The sensor spacing guarantees that at least two sensors should get a decent reading from the line during normal travel and that the line can still be detected, albeit with only one sensor at offsets of up to +/- 50mm with reasonable sensor readings. Since the linefollower itself is less than 100mm wide, that should suffice. With the follower centered over the line, the two middle sensors both see the line equally.
It would be easy enough to use those two sensors to determine the offset error but how can the rest of them be incorporated? The previous scheme relied on finding the sensor with the largest value and fitting a parabola to the readings from it and the two neighbours. This was not too hard but gave trouble at the extremes of range. The new technique is to simply create a weighted average of all the sensor readings.
Each sensor is given a weighting equal to its displacement from the center line of the mouse. Thus, their weightings, read from left to right are:
| SensorID |
0
|
1
|
2
|
3
|
4
|
5
|
| Weighting |
-37.5
|
-22.5
|
-7.5
|
7.5
|
22.5
|
37.5
|
These are just multiples of the 15mm spacing with the left side sensors given negative values and the right hand sensors given positive values.
Each sensor reading is normalised so that the recorded value is between 0 and 1000 where 1000 corresponds to it being directly over the line and 0 corresponds to it being directly over the black background.
To calculate the weighted average, each reading is multiplied by its weighting and then the sum of the weighted values is divided by the sum of the unweighted values. For example, we might have readings like these:
| SensorID |
0
|
1
|
2
|
3
|
4
|
5
|
| Weighting |
-37.5
|
-22.5
|
-7.5
|
7.5
|
22.5
|
37.5
|
| Actual Value |
9
|
494
|
789
|
37
|
0
|
0
|
| Weighted Value |
-337.5
|
-11115
|
-5917.5
|
277.5
|
0
|
0
|
The sum of the weighted values is -17092.5
The sum of the actual values is 1329
Thus, the error is -19092.5/1329 or about -12.9 indicating that we are 12.9mm off center to the right.
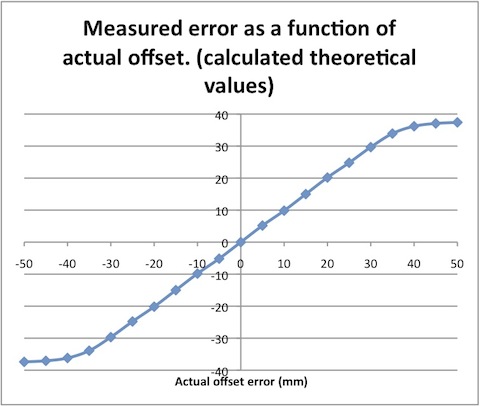
The sensitivity of the method appears good with resolution to less than 1mm available although, in a practical system, noise might reduce that. Linearity appears excellent so long as the sensors are spaced and set up to give appropriate responses like that shown above. Since the actual response will follow a slightly different distribution, the results may well be less convincing in practise.
Simulation for a range of offsets over +/- 50mm gives a response like this:
The use of a weighted average for determining the position with respect to a line if far from original. So much so that there seems little point in trying to find an original source. There are plenty of examples available from a cursory Google search.
In a practical system, the actual contest is likely to have paths that cross. Detecting such occasions would be an essential improvement to the basic task of following the line.
Noise and imperfect sensors/floors will also have a greater or larger effect on the quality of results.
Finally, since real sensors are very unlikely to give a response exactly like that shown at the top, they are unlikely to deliver such a neat linear overall response for the array. Nonetheless, it should be monotonic. That is, increasing the offset will increase the measured error across the entire working range of the sensor. Thus it should be relatively easy to generate a steering function from the result.